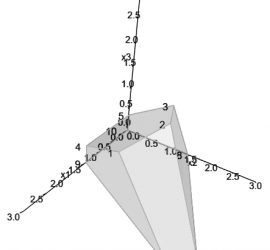
R package gMOIP has been updated to version 1.3.0 and now can plot 3D models too. The package can make 2D and 3D plots of the polytope of a linear programming (LP), integer linear programming (ILP) model, or mixed integer linear programming (MILP) model with 2 or 3 variables, including integer points, ranges and iso profit curve. Moreover you can also make a plot of the bi-objective criterion space and the non-dominated (Pareto) set for bi-objective LP/ILP/MILP programming models. Figures can be prepared for LaTeX and can automatically be transformed to TikZ using package tikzDevice.
Teaching
The last days I have been playing a bit with LocalSolver and tried to model various vehicle routing problems (VRP). LocalSolver is a heuristic solver based on a heuristic search approach combining different optimization techniques. It includes a math modeling language (LSP) and there is a package so that it can be used from R. You need to download and install LocalSolver (I used v7.0) and get an academic license from their webpage.
I recent released a small package gMOIP which can make 2D plots of linear and integer programming models (LP/IP). With the package you can make plots of the feasible region (or solution space) of an LP, visualize the integer points inside the region and the iso profit curve. Moreover, can also make a plot of a bi-objective criterion space and the non-dominated (Pareto) set. Figures are prepared for LaTeX and can automatically be transformed to TikZ using tikzDevice.
During the this semester I am teaching the course “Markov decision theory” at the Department of Mathematics. The course presents the algorithmic aspects of Markov decision theory and illustrates the wide applicability of this theory to a variety of realistic problems. First, the course consider the Poisson process followed by Renewal/Reward Processes. Next we study the theory of Markov chains. Then follows a thorough presentation of the theory of Markov Decision Processes, including some applications. Finally, further applications are discussed based on reports made by the students. A course plan is given here.
During the past months I have been participating in a course about supervision. The course, which runs over several days, covers master, PhD and fellow supervision and use results from research, practice and experiences from the participants. It aims at strengthen the participants’ overall supervisory skills in the form of clear and specific criteria-based guidance better feedback when commenting on text from the student establishment and maintenance of a mutually binding supervision agreement initial, ongoing and final project evaluation and feedback using meta-communication of supervision content and processes The course included video-filming ourselves in doing supervision which was a good way of seeing how one actually perform. The course can be recommended to all university staff doing supervision.
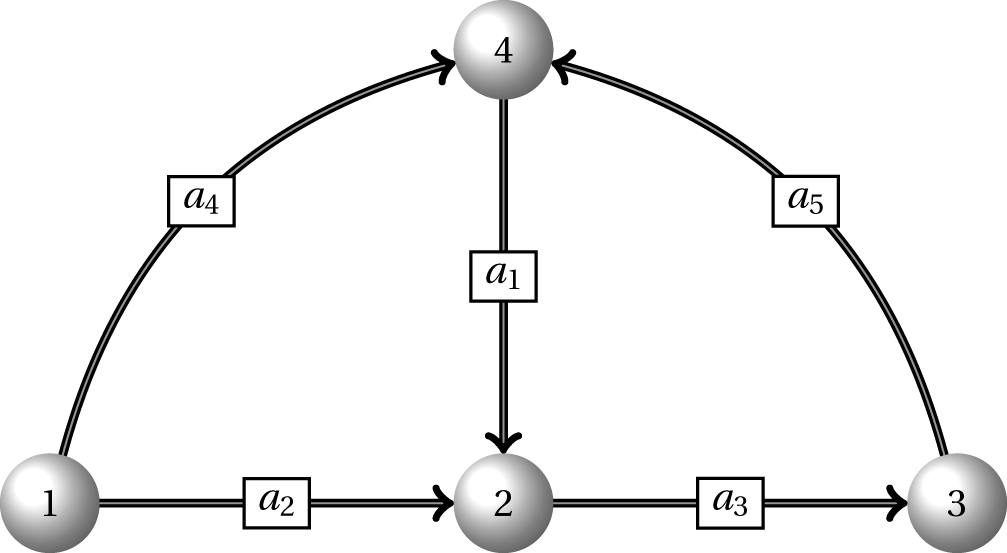
Often when I teach students at our Business School they have a hard time understanding compact linear programming (LP) formulations. So here it is, a short introduction to some of the concepts you need to know for understanding compact LP formulations. Sets A set is a group of elements, e.g. $\{1,2,4\}$ is a set with 3 elements, namely, $1,2$ and $4$ and $A=\{(2,3),(4,5),(6,8),(5,6)\}$ is a set called $A$ with 4 elements (pairs), namely, $(2,3),(4,5),(6,8)$ and $(5,6)$. Note that in the last case each element is a pair $(i,j)$. Sets containing pairs are often used when we formulate LPs based on network problems where the pair $(i,j)$ denote the arc/edge from node $i$ to node $j$.
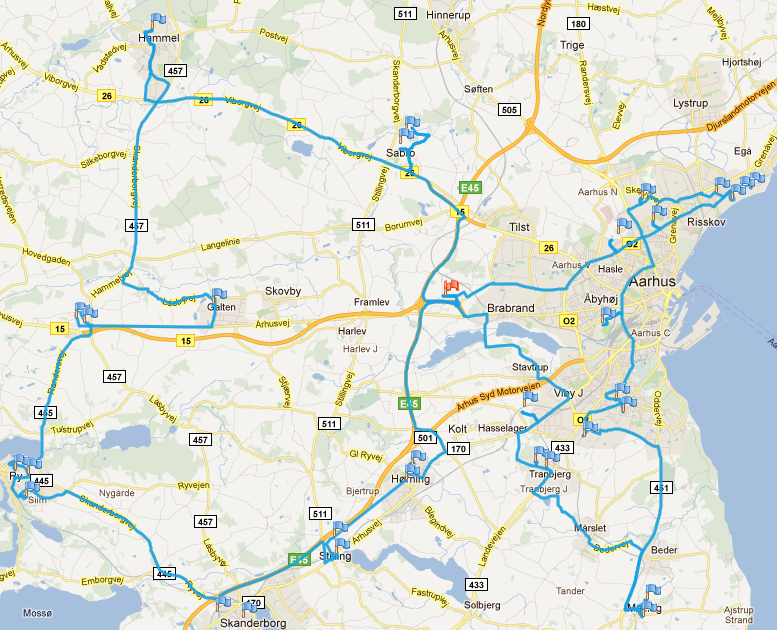
In my recent course on transportation and distribution systems for undergraduate business students I used a week talking about vehicle routing problems (VRP). Since their math skills aren’t that high the focus was not on algorithms instead I tried to talk about the general structure of the problem. Here the site logvrp.com is very good and provide a way of making a realistic problem case. Logvrp is a web based vehicle route planner software cable of minimize transportation costs and to minimize fleet mileages. It uses Google maps to display routes and trips. Moreover, it supports many different VRP problems. Current two heuristics are implemented and can be run simultaneously on a problem instance. This is a good thing since the students can see that the heuristics behave differently on the same instance and that there is no general winner. I created an exercise about a small-sized company located in […]
During the fall 2011 I have been teaching the course “Transportation and distribution systems” an optional course for undergraduate students. We have considered various topics within transportation such as its role in the global economy, modal choice, 3PL, VRP problems, flow problems, airline management, ITS, green logistics etc. Each week the students was given an exercise where they in most cases had to formulate and solve an mathematical programming model. I also have tried to introduce CPLEX OPL studio to them with minor success. Mostly they like to formulate their models in Excel and with OpenSolver it is possible even for quite large models.
Yesterday I participated in a short course about how to teach large classes. Focus was on how to align teaching for constructive learning, collaborative learning techniques and other active learning tricks. The main point can be summarized in this statement “If students are to learn desired outcomes in a reasonably effective manner, then the teacher’s fundamental task is to get students to engage in learning activities that are likely to result in their achieving those outcomes… It is helpful to remember that what the student does is actually more important in determining what is learned than what the teacher does.” (Shuell, 1986: 429)
Just finished my last Management Science lecture for this semester. This is the first time I theach this introductory course to Business Students. Topics are linear and integer programming, goal programming, simulation and network models.