Nicolas my PhD student has just finished his defense of his thesis titled “Solution algorithms for multi-objective integer linear programming models“. I would like to congratulate Nicolas with his PhD title and for a good presentation at the defense.
Lars Relund Nielsen
The research paper “Warm-starting lower bound set computations for branch-and-bound algorithms for multi objective integer linear programs” have been published in European Journal of Operational Research. Abstract: In this paper we propose a generic branch-and-bound algorithm for solving multi-objective integer linear programming problems. In the recent literature, competitive frameworks has been proposed for bi-objective 0–1 problems, and many of these frameworks rely on the use of the linear relaxation to obtain lower bound sets. When increasing the number of objective functions, however, the polyhedral structure of the linear relaxation becomes more complex, and consequently requires more computational effort to obtain. In this paper we overcome this obstacle by speeding up the computations. To do so, in each branching node we use information available from its father node to warm-start a Bensons-like algorithm. We show that the proposed algorithm significantly reduces the CPU time of the framework on several different problem […]
The research paper “Optimizing pig marketing decisions under price fluctuations” have been published in Annals of Operations Research. Abstract: In the manufacturing of fattening pigs, pig marketing refers to a sequence of culling decisions until the production unit is empty. The profit of a production unit is highly dependent on the price of pork, the cost of feeding and the cost of buying piglets. Price fluctuations in the market consequently influence the profit, and the optimal marketing decisions may change under different price conditions. Most studies have considered pig marketing under constant price conditions. However, because price fluctuations have an influence on profit and optimal marketing decisions it is relevant to consider pig marketing under price fluctuations. In this paper we formulate a hierarchical Markov decision process with two levels which model sequential marketing decisions under price fluctuations in a pig pen. The state of the system is based on […]
The research paper “Biobjective Branch-and-Cut Algorithms Based on LP Relaxation and Bound Sets” have been published in Informs Journal on Computing Abstract: Most real-world optimization problems are of a multi-objective nature, involving objectives which are conflicting and incomparable. Solving a multi-objective optimization problem requires a method which can generate the set of rational compromises between the objectives. In this paper, we propose two distinct bound set based branch-and-cut algorithms for bi-objective combinatorial optimization problems, based on implicitly and explicitly stated lower bound sets, respectively. The algorithm based on explicitly given lower bound sets computes for each branching node a lower bound set and compares it to an upper bound set. The implicit bound set based algorithm, on the other hand, fathoms branching nodes by generating a single point on the lower bound set for each local nadir point. We outline several approaches for fathoming branching nodes and we propose an […]
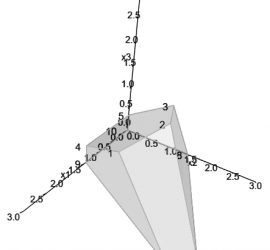
R package gMOIP has been updated to version 1.3.0 and now can plot 3D models too. The package can make 2D and 3D plots of the polytope of a linear programming (LP), integer linear programming (ILP) model, or mixed integer linear programming (MILP) model with 2 or 3 variables, including integer points, ranges and iso profit curve. Moreover you can also make a plot of the bi-objective criterion space and the non-dominated (Pareto) set for bi-objective LP/ILP/MILP programming models. Figures can be prepared for LaTeX and can automatically be transformed to TikZ using package tikzDevice.
From November 4-7, 2018 we have been participating the annual INFORMS conference, Phoenix, AZ, US. Talks have been interesting and for the first time CORAL joined the job fair to promote open Assistant and Associate Professor positions. The interest was overwhelming and some good candidates were found.
The research paper “An improved cut-and-solve algorithm for the single-source capacitated facility location problem” have been published in EURO Journal on Computational Optimization. Abstract: In this paper, we present an improved cut-and-solve algorithm for the single-source capacitated facility location problem. The algorithm consists of three phases. The first phase strengthens the integer program by a cutting plane algorithm to obtain a tight lower bound. The second phase uses a two-level local branching heuristic to find an upper bound, and if optimality has not yet been established, the third phase uses the cut-and-solve framework to close the optimality gap. Extensive computational results are reported, showing that the proposed algorithm runs 10–80 times faster on average compared to state-of-the-art problem-specific algorithms.
The past weeks we have created Multi-Objective Optimization Repository (MOrepo) which is a response to the needs of researchers from the MCDM society to access multi-objective (MO) optimization instances. The repository contains instances, results, generators etc. for different MO problems and is continuously updated. The repository can be used as a test set for testing new algorithms, validating existing results and for reproducibility. All researchers within MO optimization are welcome to contribute. For more information see https://github.com/MCDMSociety/MOrepo.
The last days I have been playing a bit with LocalSolver and tried to model various vehicle routing problems (VRP). LocalSolver is a heuristic solver based on a heuristic search approach combining different optimization techniques. It includes a math modeling language (LSP) and there is a package so that it can be used from R. You need to download and install LocalSolver (I used v7.0) and get an academic license from their webpage.
I recent released a small package gMOIP which can make 2D plots of linear and integer programming models (LP/IP). With the package you can make plots of the feasible region (or solution space) of an LP, visualize the integer points inside the region and the iso profit curve. Moreover, can also make a plot of a bi-objective criterion space and the non-dominated (Pareto) set. Figures are prepared for LaTeX and can automatically be transformed to TikZ using tikzDevice.