This post is a guide on how to install the computer typesetting system LaTeX and the corresponding programs for editing and creating LaTeX documents, and converting them to Portable Document Format (pdf) on Windows. You will need to install the following software in the following order A LaTeX engine. A free engine under Windows is MikTeX (containing a lot of other useful stuff). Just install the basic installer, which will download the packages you need automatically. A LaTeX editor. I recommend the free editor TeXStudio which is very powerful. Download and install the latest version. If you want another spellchecker language (e.g. Danish), have a look at this page. Even though that TeXStudio have a built-in pdf viewer. I also suggest to install SumatraPDF. Happy typing 🙂
Lars Relund Nielsen
During the this semester I am teaching the course “Markov decision theory” at the Department of Mathematics. The course presents the algorithmic aspects of Markov decision theory and illustrates the wide applicability of this theory to a variety of realistic problems. First, the course consider the Poisson process followed by Renewal/Reward Processes. Next we study the theory of Markov chains. Then follows a thorough presentation of the theory of Markov Decision Processes, including some applications. Finally, further applications are discussed based on reports made by the students. A course plan is given here.
One of my PhD students, for who I am a co-supervisor, has just finished the defense of her thesis titled “Methods for Sensor Based Farrowing Prediction and Floor-heat Regulation: The Intelligent Farrowing Pen“. I would like to congratulate Aparna with her PhD title and for a good thesis and presentation at the defense. I have included the thesis summary below.
The research paper “Ranking paths in stochastic time-dependent networks” have been accepted for publication in European Journal of Operational Research. In this paper we address optimal routing problems in networks where travel times are both stochastic and time-dependent. In these networks, the best route choice is not necessarily a path, but rather a time-adaptive strategy that assigns successors to nodes as a function of time. Nevertheless, in some particular cases an origin-destination path must be chosen a priori, since time-adaptive choices are not allowed. Unfortunately, finding the a priori shortest path is an NP-hard problem. We propose a solution method for the a priori shortest path problem, and we show that it can be easily extended to the ranking of the first K shortest paths. Our method exploits the solution of the time-adaptive routing problem as a relaxation of the a priori problem. Computational results are presented showing that, under […]
From 17-22 June 2013 I have been participating in MCDM 2013 in Malaga. The 22nd International Conference on Multiple Criteria Decision Making. The conference was held in a nice atmosphere and the city can be recommended. I coauthored a talk about the Bicriterion Stochastic Knapsack Problem which is a problem we currently are working on.
During the past months I have been participating in a course about supervision. The course, which runs over several days, covers master, PhD and fellow supervision and use results from research, practice and experiences from the participants. It aims at strengthen the participants’ overall supervisory skills in the form of clear and specific criteria-based guidance better feedback when commenting on text from the student establishment and maintenance of a mutually binding supervision agreement initial, ongoing and final project evaluation and feedback using meta-communication of supervision content and processes The course included video-filming ourselves in doing supervision which was a good way of seeing how one actually perform. The course can be recommended to all university staff doing supervision.
The research paper “Inventory control in a lost-sales setting with information about supply lead times” have been accepted for publication in International Journal of Production Economics. We consider a periodically reviewed single-item inventory system in a lost sales setting where at most one order can be outstanding at a time and compare the performance of an inventory model assuming informed lead times to a model assuming uninformed independent and identically distributed lead times.
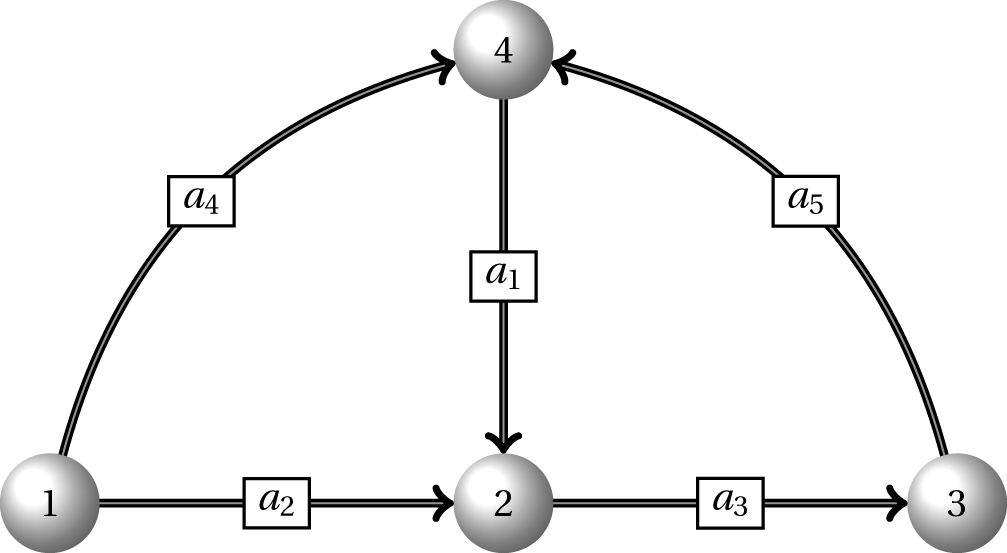
Often when I teach students at our Business School they have a hard time understanding compact linear programming (LP) formulations. So here it is, a short introduction to some of the concepts you need to know for understanding compact LP formulations. Sets A set is a group of elements, e.g. $\{1,2,4\}$ is a set with 3 elements, namely, $1,2$ and $4$ and $A=\{(2,3),(4,5),(6,8),(5,6)\}$ is a set called $A$ with 4 elements (pairs), namely, $(2,3),(4,5),(6,8)$ and $(5,6)$. Note that in the last case each element is a pair $(i,j)$. Sets containing pairs are often used when we formulate LPs based on network problems where the pair $(i,j)$ denote the arc/edge from node $i$ to node $j$.
I often hear people complain about the GPS they use for routing. Some do a better job than others. This is due to two things: the algorithm which may vary and the network used. Here I will focus on the network. Often the algorithms have to use different networks because: the network has not been updated or a different provider is used. This is illustrated in this post showing that the total length in the networks used by TomTom and OpenStreetMap are quite different. As a result the shortest path algorithm will find different optimal paths as illustrated in this post.
This is the title of a good article about the psychological principles about waiting. This is something that we as researchers in Operations Research often forget and calls for more interdisciplinary research in this area. Why Waiting Is Torture, New York Times