Often when I teach students at our Business School they have a hard time understanding compact linear programming (LP) formulations. So here it is, a short introduction to some of the concepts you need to know for understanding compact LP formulations.
Sets
A set is a group of elements, e.g. $\{1,2,4\}$ is a set with 3 elements, namely, $1,2$ and $4$ and $A=\{(2,3),(4,5),(6,8),(5,6)\}$ is a set called $A$ with 4 elements (pairs), namely, $(2,3),(4,5),(6,8)$ and $(5,6)$. Note that in the last case each element is a pair $(i,j)$. Sets containing pairs are often used when we formulate LPs based on network problems where the pair $(i,j)$ denote the arc/edge from node $i$ to node $j$.
You can take the union of sets: \[\{1,2,3\} \cup \{3,4\} = \{1,2,3,4\},\] subtract elements: \[\{1,2,3,4,5\} \setminus \{3,4\} = \{1,2,5\},\] or the intersection: \[\{1,2,3\} \cap \{3,4\} = \{3\}.\]
Some special sets are: $\emptyset=\{\}$ – the empty set, $\mathbb{N} = \{1,2,3,\ldots\}$ – the set of natural numbers, $\mathbb{N_0} = \{0,1,2,3,\ldots\}$ – the set of non-negative integers, and $\mathbb{Z} = \{ \ldots,-2,-1,0,1,2,\ldots \}$ – the set of integers.
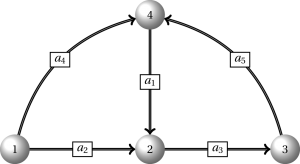
A network $G$ is described using a pair consisting of two sets $G=(V,A)$. Here $V$ denote the set of nodes and $A$ the set of arcs (if directed) or edges (if undirected). Given the network below we have that $V=\{1,2,3,4\}$ and $A=\{a_1,a_2,a_3,a_4,a_5\}=\{(4,2),(1,2),(2,3),(1,4),(3,4)\}$. Note that we write the arcs in two different ways using either elements $a_i$ or pairs. Moreover, we always have the tail of the arc as the first number in the pair.
Subsets can be described using set-builder notation: $A_3=\{(i,j)\in A : i=3 \text{ or } j=3\} =\{(i,j)\in A \mid i=3 \text{ or } j=3\} = \{(2,3),(3,4)\}$. We read it as $A_3$ equals the set of $(i,j)$ in $A$ such that (satisfying) either $i$ or $j$ equals $3$. Note symbols $:$ and $\mid$ have the same meaning (such that).
Sums based on sets
Sums may be written in different ways. Let $I=\{1,2,3,4\}$. Then we have
\[
\sum_{i\in I} x_i = \sum_{i=1}^{4} x_i = \sum_{i\in\{1,2,3,4\}} x_i = x_1+x_2+x_3+x_4.
\]
Other examples:
\[
\sum_{(i,j)\in\{(i,j)\in A : i=3 \text{ or } j=3\} } x_{ij} = \sum_{(i,j)\in A_3} x_{ij} = x_{23}+x_{34}
\]
and
\[
\sum_{(2,j)\in A} x_{2j} = x_{23}.
\]
Constraints
Often constraints are written in a compact way to avoid writing a lot of equations explicit so\[\sum_{i \in \left\{ 1,6 \right\}} x_{ij} \leq b_j,\; \forall j \in \left\{ 8,12 \right\},\] can be written explicit as
\begin{align}
x_{1,8} + x_{6,8} &\leq b_8, \\
x_{1,12} + x_{6,12} &\leq b_{12}. \\
\end{align}
Note the constraint consists of two parts: 1) the equation and 2) a part describing which index values we consider. The second part contain the $\forall$-sign which is read “for all”. Think of it as all fixed index values in the second part must be inserted in the equation one at a time. That is, we have a constraint for each combination of index in the second part. As a result a constraint where an index is both in the sum and the second part is not valid. Finally, note that sometimes $x_{ij}$ is written $x_{i,j}$ this is done to avoid confusion if the index are large, e.g. $x_{121}$ could be interpreted as $x_{1,21}$ or $x_{12,1}$.
Let us do another example: \[\sum_{(i,j)\in A} x_{ij} – \sum_{(j,i)\in A} x_{ji} \leq b_i,\; \forall i\in V. \] Here we have a constraint for each node in $V$, i.e. if we consider the network above, 4 in total. So we have to use the values $1,2,3$ and $4$ for index $i$. For $i=2$ the constraint becomes:
\[
\sum_{(2,j)\in A} x_{2j} – \sum_{(j,2)\in A} x_{j2} = x_{23} – (x_{12}+x_{42}) \leq b_{2}.
\]
Similar for $i=1,3,4$ we have:
\begin{align}
x_{14} +x_{12} &\leq b_{1}, \\
x_{34} – x_{23} &\leq b_{3}, \\
x_{42} – x_{14}-x_{34} &\leq b_{4}. \\
\end{align}
Last example: \[\sum_{(i,j)\in A} x_{ij}+y_k \leq z_i,\; \forall i\in V, k=1,4. \] We have $4\cdot 2=8$ constraints which are:
\begin{align}
x_{14} +x_{12}+y_1 &\leq z_{1} \text{ ($i=1$ and $k=1$),} \\
x_{23} +y_1 &\leq z_{2} \text{ ($i=2$ and $k=1$),} \\
x_{34} +y_1 &\leq z_{3} \text{ ($i=3$ and $k=1$),} \\
x_{42} +y_1 &\leq z_{4} \text{ ($i=4$ and $k=1$),} \\
x_{14} +x_{12}+y_4 &\leq z_{1} \text{ ($i=1$ and $k=4$),} \\
x_{23} +y_4 &\leq z_{2} \text{ ($i=2$ and $k=4$),} \\
x_{34} +y_4 &\leq z_{3} \text{ ($i=3$ and $k=4$),} \\
x_{42} +y_4 &\leq z_{4} \text{ ($i=4$ and $k=4$).} \\
\end{align}